지난 글에 이어서 이번에 쓸 알고리즘은 DBSCAN 입니다. Density-Based Spatial Clustering of Applications with Noise 의 약자라고 하는데, 결론적으로 말해서 클러스터의 갯수를 정하지 않아도 된다라는 거 빼고는 엄청난... 뭐랄까 장점은 없어 보이네요

지난 글에서 클러스터링 기법 중에 가장 기초적인 K-means clustering을 소개했었습니다.
데이터 분류 (클러스터링) 기법 : K-means clustering
데이터 분류 (클러스터링) 기법이 뭐가 엄청 많은데, 이제부터 하나씩 공부해 가면서 정리 겸 블로그에 남기려고 합니다. 그 첫번째로 가장 기초적이고 가장 쉬운 K-means clustering부터 시작해 볼께
guzene.tistory.com
K-means 클러스터링의 아이디어가 너무나 간단하기 때문에, DBSCAN이라는 뭔가 약자를 이어붙인 것에서 굉장히 거창할 줄 알았는데, 그렇지는 않습니다.
하...
경어체를 사용하려고 노력했었는데 뭔가 계속 어색하네요. 그냥 구어체랑 섞어서 막 할께요! 하던대로 해야지 이거 원
좋아 일단 위키 등으로 파악한 과정을 한 번 살펴보자 (어우 말투 편해)
1. 데이터들 중에 하나를 잡고 일정한 반경 안에 있는 포인트들은 같은 클러스터로 정의함
1-1. 이때 두개 조건을 정해줘야 하는데, "일정한 반경" 즉 반경을 정해줘야 하고
1-2. "있는 포인트들" 즉, 포인트의 최소 갯수를 정해줘야 한다.
2. 조건에 만족하지 못하면 지금 탐색했던 포인트는 클러스터를 이루지 못하고 노이즈로 빠짐
3. 이런 식으로 모든 포인트에 대해 클러스터에 해당되는지를 정함
K-means clustering은 오히려 스텝 바이 스텝으로 되어 있어서 명확했는데, 이건 코드로 살펴보는 게 나을 거 같은 느낌이 든다. 그런데, DBSCAN의 결정적인 단점 중에, "잘 작동하지 않는다" 라는 것이 있었는데, 그래서 이게 내가 코드를 잘못 짠 건지 원래 이런 건지 구분이 너무 애매해서... sklearn 라이브러리에서 제공하는 결과와 비교도 해보겠다.
먼저 코드를 스텝으로 살펴보자
필요한 라이브러리
# coding: utf-8
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN이건 그냥 넘어갈게요...
데이터셋 만들기
num_data = 300
dimension = 2
data = np.random.randn(num_data, dimension)
offsets = np.array([[5,2], [-1,5], [2,3], [5,5], [-4,0], [4,-3],[6,8]])
# offsets = np.array([[6,8], [-6,-8], [-6,8], [6,-8]])
for offset in offsets:
data = np.append(data,np.random.randn(num_data, dimension)*1.2 + offset, axis=0)
fig = plt.figure(figsize=[10,10])
plt.scatter(data.T[0],data.T[1], s=6)
plt.grid()
plt.show()임의로 데이터셋을 만드는 코드. 가우시안 분포의 덩어리를 여기저기 오프셋을 주고 만들어준다. 위 코드로 생성된 데이터를 플랏해보면 아래와 같다.

솔직히 사람 눈에는 그래도 뭉터기가 좀 보이는데. 내가 만들어서 그런가? 아무튼 이걸로 진행해보자
클러스터링
eps = 1.5 # 하나의 클러스터라고 할 거리를 정함
min_samples = 5 # 최소한 이거 이상의 인자만 속하면 클러스터다!
cluster = np.zeros(len(data), dtype=np.int64)-1 # 클러스터 할당 초기화
index = np.arange(len(data))
for i in range(len(data)):
cluster_max = np.max(cluster, axis=0) # 클러스터의 최대값
diff = data - data[index[i]]
dist = np.sum(diff*diff, axis=1)
dist = np.sqrt(dist)
cluster_now = cluster[index[i]] # 현재 데이터의 클러스터를 구함
# 거리가 지정한 값 이내에 있는 점들의 클러스터를 구하고
# 이의 최대값을 구함. 즉, 클러스터가 -1이 아니라 다른 것으로 할당된 적이 있는가를 확인
cluster_next = np.max(cluster[np.where(dist < eps)[0]], axis=0)
# 반경 안에 최소 샘플 이상이 속할 때만 뭔가를 할 수 있음
if np.sum(dist < eps) >= min_samples:
# 주변 점부터 탐색할 수 있도록 인덱스 순서를 바꿈
index = np.append(np.where(dist < eps)[0], np.where(dist >= eps)[0], axis=0)
if cluster_next == -1: # 주변 점들 모두가 클러스터를 할당받은 적이 없을 때
# 거리가 일정 이하인 점들에게 이제까지 할당한 적 없는 클러스터를 할당
cluster[np.where(dist < eps)[0]] = cluster_max + 1
searched[np.where(dist < eps)[0]] = 1
else: # 누군가 할당을 받았을 때
# 거리가 일정 이하인 점들에게 어딘가의 점이 할당된 클러스터를 할당
cluster[np.where(dist < eps)[0]] = cluster_next
# 클러스터에서 중복을 제거하고 할당된 클러스터가 뭐가 있는지 구함
cluster_number = list(set(list(cluster.tolist()))) 어느 정도 학습을 반복하면서 진행했던 K-means clustering과는 조금 방식이 다르다. 루프를 돌긴 하지만 그냥 점점마다 진행하는 것으로... 주석을 최대한 자세히 달아놨는데, 일단 한번 결과를 볼까?
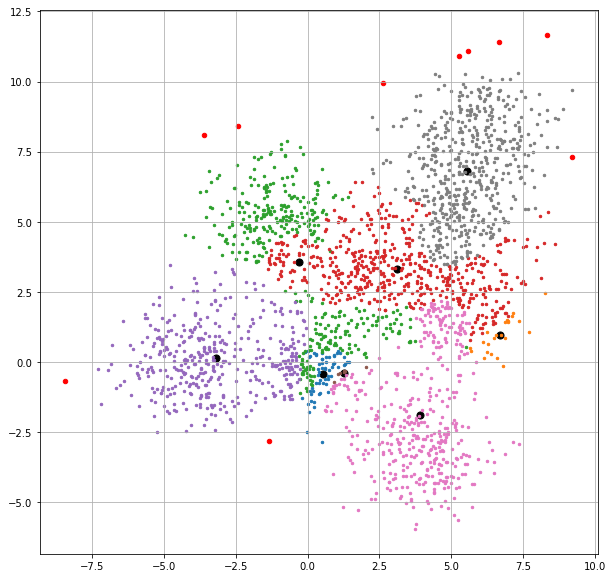
아니 솔직히 이게 거의 비슷한 데이터라도, 데이터를 재생성하면 (재생성하는 방식이 randn 이다 보니) 클러스터링이 완전히 달라진다. 똑같은 조건으로 재생성해볼까?

코드를 잘못 짠건가... 싶어서 이번엔 sklearn으로 돌려보자
클러스터링 두번째 : sklearn
eps = 0.5 # 하나의 클러스터라고 할 거리를 정함
min_samples = 5 # 최소한 이거 이상의 인자만 속하면 클러스터다!
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
cluster = dbscan.fit_predict(data)
cluster_number = list(set(list(cluster.tolist())))코드는 초간단. 역시 라이브러리는 라이브러리!! (요새 누가 날코딩하나?)

장난하는 것도 아니고 ㅋㅋㅋㅋㅋ 이게 뭐냐고...
아니 DBSCAN이라는 게 이렇게 형편없는 거였어?? 라는 생각이 들어서, 이번엔 하기 좋은 데이터를 한번 띄워봤다

이거도 못하면 바보지 그냥 못쓰는 거다!! 라고 생각하고 해본 결과는 아래와 같다.

이 결과는 날코딩한 거나 sklearn 쓴 거나 비슷하다. 아니 뭐... 당연히 그렇겠지요
그래서 장점이 뭐야?
아니 그래서 대체 장점이 뭐냐... 라고 생각했을 때, 솔직히 k-means clustering은 위의 데이터처럼 구분하기 좀 어려운 것도 어느 정도 구분을 잘 해준다. 단지 최대의 단점이 클러스터의 갯수를 정해줘야 한다는 건데 DBSCAN의 장점은 바로 그 지점 아니겠어?
즉, 다닥다닥 붙어있는 데이터만 아니라면, 상당히 뭐랄까... 아 적당히 알아서 해 주네 라는 느낌으로 쓸 수 있다는 거? 아 근데 생각보다... 실망스러워서 ㅋㅋㅋㅋ 구글링해보면 진짜 거침없이 클러스터링 해대는 느낌이었는데 말입니다.
어쨌든 이걸로 DBSCAN도 독파! 그래도 대충 어느 경우에 써야 하는지는 알겠다. 다음에는 Expectation-Maximization 관련된 EM-GMM 알고리즘을 들고 오겠어요




댓글